Collins Cambridge International AS & A Level Further Mathematics 是柯林斯出版社(Collins)为剑桥国际AS & A Level进阶数学课程(课程代码:9231)设计的权威教材系列,专为数学能力突出、计划深入探索数学领域的学生打造。该教材以 “理论深度+考试实战” 为核心,系统覆盖纯数学、力学与统计学的高阶内容,旨在为大学STEM专业(如数学、工程、物理、计算机科学)奠定坚实基础。




教材概况
- 课程适配:
- 严格遵循 剑桥国际AS & A Level进阶数学教学大纲(9231),需在完成A Level数学(课程代码:9709)后选修。
- 适配考试模块:Further Pure Mathematics(纯数学进阶)、Further Mechanics(力学进阶)、Further Probability & Statistics(统计进阶)。
- 核心理念:
- “抽象思维+现实建模”:通过数学理论与实际问题的无缝衔接,培养高阶分析与创新能力。
- “考试导向”:融入大量真题解析与评分标准,精准对标高分策略。

教材分册与内容模块
系列按学科模块分为 三册,学生可根据考试要求灵活组合学习:
| 教材分册 | 覆盖内容 | 适用考试模块 |
|---|---|---|
| Further Pure Mathematics 1 | 复数、矩阵与线性代数、数学归纳法、极坐标系、微分方程初步。 | AS/A Level 纯数学核心模块 |
| Further Pure Mathematics 2 | 双曲函数、向量空间、群论基础、微分方程进阶、数值方法。 | A Level 纯数学扩展模块 |
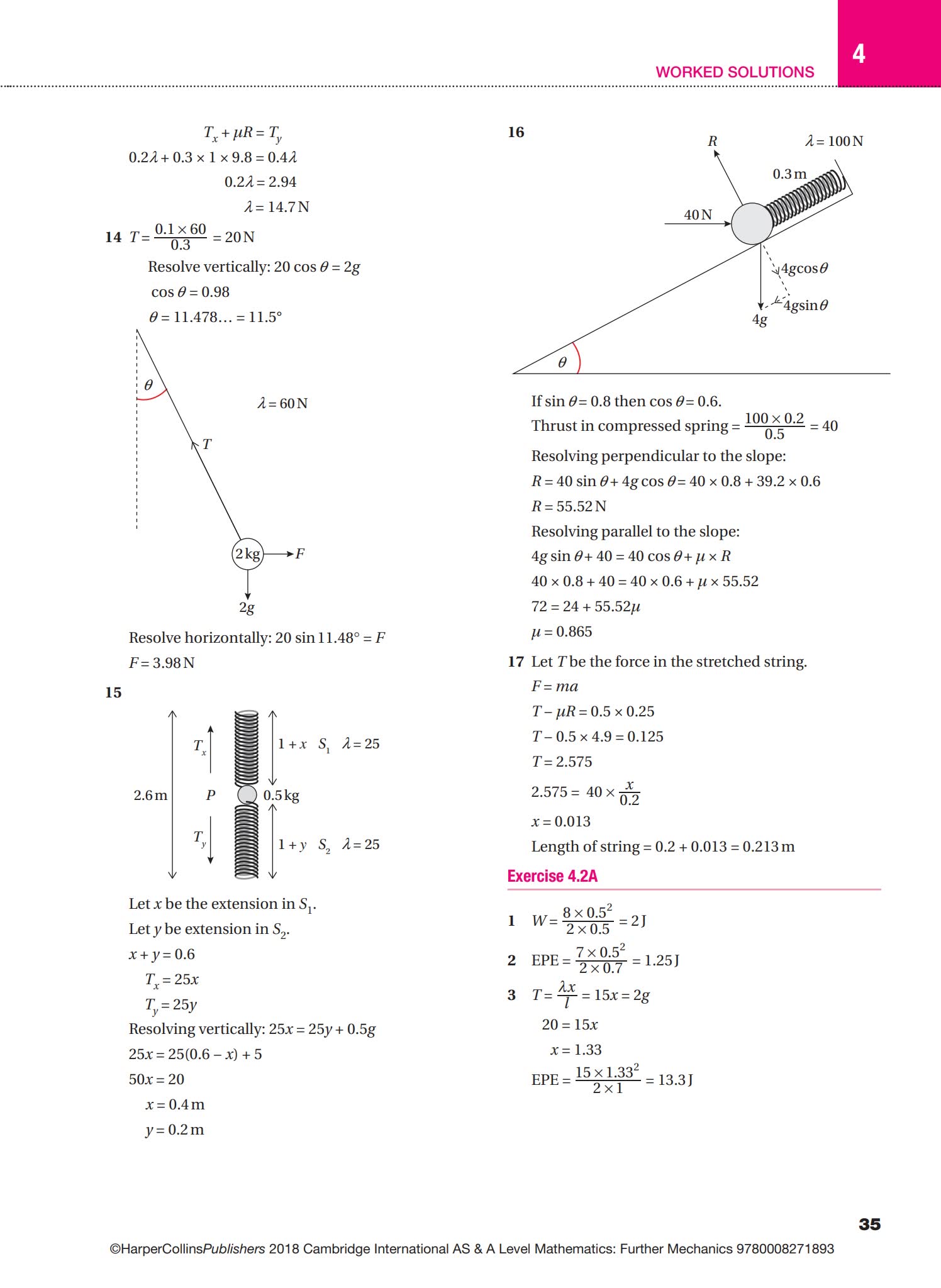
| Further Mechanics | 刚体静力学、圆周运动动力学、简谐运动(SHM)、动量与能量进阶分析。 | AS/A Level 力学模块 |
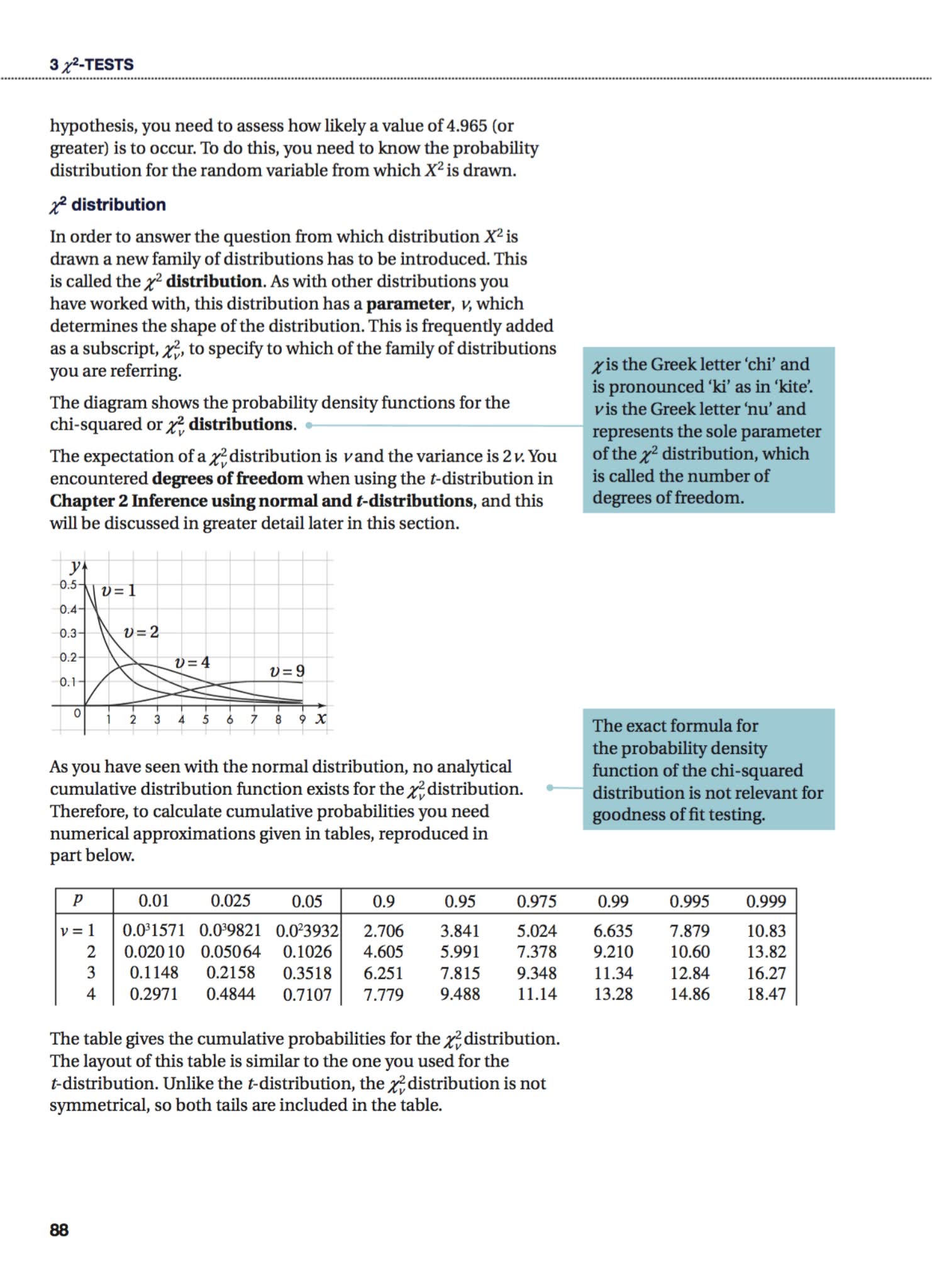
| Further Probability & Statistics | 连续概率分布(正态、指数)、统计推断进阶(假设检验、卡方检验)、回归模型、随机过程基础。 | AS/A Level 统计模块 |
核心特色与教学内容
理论深度与逻辑拆解

- 抽象概念具象化:
- 通过几何图解解释复数运算(如复平面旋转)、矩阵变换(如三维空间投影)。
- 群论(Group Theory)以对称性实例引入(如分子结构、艺术图案)。
- 分步推导教学:
- 微分方程求解步骤拆解(如分离变量法、积分因子法),标注易错点(如常数项处理)。

跨学科应用与技术整合
- 现实建模案例:
- 刚体静力学分析桥梁结构稳定性。
- 微分方程模拟传染病传播(如SIR模型)。

适用人群
- 学术目标明确的尖子生:
- 计划在大学攻读 数学、理论物理、金融工程、人工智能 等需要高阶数学能力的专业。
- 目标参加 STEP、MAT、AIME 等大学入学数学竞赛的学生。
- 国际学校与教师:
- 需系统教授进阶数学课程的教师,寻求标准化教案与考试资源。
- 自学者与备考机构:
- 具备扎实A Level数学基础(建议至少达到A/A*),希望自修进阶内容的学生。

使用建议
学生学习策略

- 分阶段学习计划:
- AS阶段:完成Further Pure Mathematics 1 + 一门应用模块(力学/统计),每周投入5-6小时。
- A Level阶段:深化Further Pure Mathematics 2,结合第二应用模块,强化真题训练。
- 错题管理与复盘:
- 建立“错题档案”,分类记录逻辑漏洞(如群论公理理解偏差)与计算失误(如矩阵乘法顺序错误)。
- 技术工具辅助:
- 使用Wolfram Alpha验证复杂积分结果,或通过Excel进行统计模拟(如蒙特卡洛方法)。
资源目录
- Colins Cambridge International AS A Level Further Mathematics Further Probability and Statistics.pdf
- Collins Cambridge International AS A Level Further Mathematics Further Pure Mathematics 1.pdf
- Collins Cambridge International As A Level Further Mathematics Further Pure Mathematics 2.pdf
- Collins Cambridge International As A Level Further Mathematics Further Mechanics.pdf
Collins Cambridge International AS & A Level Further Mathematics 是国际数学教育的标杆教材,其 模块化设计、真题导向与跨学科整合 助力学生突破传统数学边界。它不仅为大学STEM专业铺路,更通过批判性思维与建模能力训练,培养解决复杂现实问题的未来创新者。





